Exponenciação usando laços em C++

Neste tutorial de nosso curso de C++, vamos aprender como usar laços para criar a operação matemática de exponenciação.

Exponenciação na Matemática

Chamamos de exponenciação, a operação matemática que tem dois números: a base e o expoente.
É o famoso 'x elevado a y'.

Por exemplo:
3² (3 elevado a 2, ou 3 elevado ao quadrado) - 3 é base e 2 o expoente
4³ (4 elevado a 3, ou 4 ao cubo) - 4 é a base e 3 o expoente.

Agora calculando essas operações:
3² = 3 * 3 = 9
4³ = 4 * 4 * 4 = 64
5⁴ = 5 * 5 * 5 * 5 = 625

Note como o valor da base se repete o tanto de vezes o valor do expoente...se repete...huuuum...repetição...lembra o quê? Huuum, laços!

Exponenciação com laços no C++

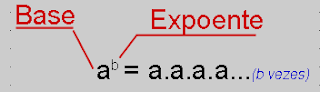
Se temos um valor:
a^b (a elevado a b), isso significa que o valor de a vai se repetir b vezes:

Vamos pedir ao usuário as variáveis base e expo.
O resultado, vamos armazenar em res, esse valor é inicializado com 1, pois vamos fazer uma série de multiplicações nessa variável.

Dentro do laço FOR, temos uma variável auxiliar aux que vai contar de 1 até expo, para realizar expo repetições, concorda?

Veja como fica nosso código usando laço FOR:

#include <iostream>
using namespace std;

int main()
{
    int base, expo, res=1, aux;

    cout << "Base: ";
    cin >> base;

    cout << "Expoente: ";
    cin >> expo;

    for(aux=1 ; aux<=expo ; aux++)
        res *= base;

    cout <<base<<"^"<<expo<<" = "<<res<<endl;

    return 0;
}

Agora com laço WHILE:

#include <iostream>
using namespace std;

int main()
{
    int base, expo, res=1, aux=1;

    cout << "Base: ";
    cin >> base;

    cout << "Expoente: ";
    cin >> expo;

    while(aux<=expo){
        res *= base;
        aux++;
    }

    cout <<base<<"^"<<expo<<" = "<<res<<endl;

    return 0;
}

E por fim, com a estrutura de repetição DO WHILE (basta digitar 0 e/ou 0 para encerrar os cálculos):

#include <iostream>
using namespace std;

int main()
{
    int base, expo, res, aux;

    do{
        cout << "Base: ";
        cin >> base;

        cout << "Expoente: ";
        cin >> expo;

        res=1;
        for(aux=1 ; aux<=expo ; aux++)
            res *= base;

        cout <<base<<"^"<<expo<<" = "<<res<<endl;
        cout<<endl;
    }while(base || expo);

    return 0;
}

Obviamente, esse algoritmo funciona apenas para expoentes inteiros, para decimais, o buraco é mais embaixo.

Mas vejam que bacana, a utilidade e versalidade das estruturas de repetição, nossos amados laços, servem até para fazer operações matemáticas.